Gradient Là Gì Trong Toán Học? Hỏi Đáp

Gradient trong toán học là một khái niệm quan trọng thường được sử dụng trong nhiều lĩnh vực, đặc biệt là trong tối ưu hóa và máy học. Bài viết này sẽ giải đáp câu hỏi “Gradient Là Gì Toán Học” thông qua việc phân tích khái niệm, ứng dụng và cách tính toán gradient.

Khái Niệm Gradient

Gradient Là Gì?

Gradient là một vector chứa các đạo hàm riêng phần của một hàm số đa biến. Đạo hàm riêng phần biểu thị tốc độ thay đổi của hàm số theo từng biến số riêng lẻ. Gradient cho biết hướng và tốc độ lớn nhất mà giá trị của hàm số tăng lên tại một điểm cụ thể trong không gian.

Tính Chất Của Gradient

Gradient được thể hiện bằng ký hiệu ∇f(x), trong đó f là hàm số và x là điểm xét trong không gian. Các tính chất quan trọng của gradient bao gồm:

Hướng Tăng Nhanh Nhất: Gradient chỉ ra hướng mà hàm số tăng nhanh nhất.
Tối Ưu Hóa: Trong các phương pháp tối ưu hóa, gradient thường được sử dụng để tìm cực đại hoặc cực tiểu của hàm số.

Ứng Dụng Gradient Trong Tối Ưu Hóa

Phương Pháp Gradient Descent

Gradient Descent là một thuật toán sử dụng gradient để tìm cực tiểu của một hàm số. Quy trình chung bao gồm việc xuất phát từ một điểm gần cực tiểu, tính gradient tại điểm đó và điều chỉnh theo hướng nghịch đảo của gradient với một bước tiến phù hợp (learning rate).

Công thức cập nhật điểm trong Gradient Descent là:

[ theta{t+1} = theta{t} – eta cdot nabla_{theta} f(theta_t) ]

Trong đó:

(theta_t) là điểm hiện tại.
(nabla_{theta} f(theta_t)) là gradient của hàm số tại (theta_t).
(eta) là learning rate, điều chỉnh bước đi trong thuật toán.

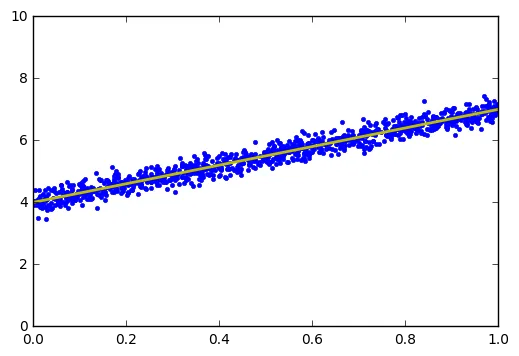Minh họa gradient với đường đồng mức trong tối ưu hóa

Hình ảnh: Minh họa gradient với đường đồng mức trong tối ưu hóa sử dụng gradient descent.

Ví Dụ Cụ Thể

Xét hàm số f(x, y) = (x^2 + y – 7)^2 + (x – y + 1)^2. Gradient của hàm này đóng vai trò quan trọng trong việc tìm các điểm mà tại đó hàm đạt giá trị cực tiểu. Điểm (2,3) và (-3,-2) trong không gian là hai điểm global minimum của hàm số.

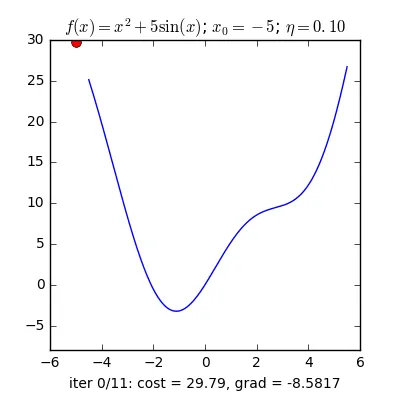Minh họa kết quả Gradient Descent

Hình ảnh: Minh họa kết quả của thuật toán Gradient Descent với hình ảnh đồ thị minh họa.

Tổng Kết và Giải Pháp

Gradient là công cụ mạnh mẽ trong toán học, đặc biệt trong lĩnh vực tối ưu hóa và máy học. Nó giúp xác định hướng tối ưu để điều chỉnh các tham số nhằm đạt được giá trị lớn nhất hoặc nhỏ nhất của hàm số. Việc hiểu và áp dụng gradient một cách hiệu quả có thể cải thiện đáng kể khả năng giải quyết các bài toán phức tạp trong thực tế.

Để tìm hiểu thêm về ứng dụng cụ thể của gradient trong học máy, mời bạn theo dõi các bài viết và phần học liệu liên quan trên trang web của Trường THPT Chuyên Nguyễn Tất Thành.

Tài Liệu Tham Khảo

A Comprehensive Guide to Machine Learning – Online.
Đạo hàm và Gradient – Sách giáo khoa Toán cao cấp.
Các tài liệu học tập tại Trường THPT Chuyên Nguyễn Tất Thành.