3 Đường Thẳng Đồng Quy Là Gì?

Có khi nào bạn tự hỏi “3 đường Thẳng đồng Quy Là Gì?” Đây không chỉ là khái niệm quan trọng trong hình học mà còn mang lại nhiều ứng dụng thực tiễn. Bài viết này sẽ giải đáp thắc mắc của bạn và cung cấp cái nhìn sâu rộng hơn về lý thuyết và các ứng dụng của khái niệm đồng quy.

Đồng Quy Là Gì?

Đồng quy là thuật ngữ dùng để mô tả ba hoặc nhiều đường thẳng cắt nhau tại một điểm duy nhất, được gọi là điểm đồng quy. Tính chất này rất quan trọng trong giải quyết các bài toán liên quan đến tam giác và các dạng hình học khác. Ngoài ra, đồng quy còn có ứng dụng rộng rãi trong các lĩnh vực như kiến trúc, giao thông, và khoa học tự nhiên.

Đồng quy là việc ba hoặc nhiều đường thẳng giao nhau tại một điểm

Các Trường Hợp Đồng Quy Thường Gặp

Đồng quy không chỉ nằm trong tam giác mà còn hiện diện trong nhiều dạng hình học khác nhau.

Đồng Quy Trong Tam Giác

Trong tam giác, 3 đường đồng quy có thể là trung tuyến, phân giác, trung trực, hoặc đường cao từ đỉnh tam giác đó.

Đồng Quy Trong Hình Tròn

Các đường kính của một đường tròn luôn đồng quy tại tâm của nó, trong khi các tiếp tuyến từ một điểm bên ngoài cũng gặp nhau tại điểm tiếp xúc.

Một số trường hợp đồng quy thường gặp

Phương Pháp Chứng Minh Đồng Quy

Chứng minh 3 đường thẳng đồng quy là một kỹ năng quan trọng trong hình học. Dưới đây là một số phương pháp phổ biến:

Tìm Điểm Cắt Nhau: Xác định điểm cắt của hai đường thẳng và chứng minh đường thẳng còn lại đi qua điểm đó.
Áp Dụng Tính Chất Đặc Biệt: Sử dụng các tính chất đặc biệt của tam giác hoặc hình học để chứng minh.
Dùng Phản Chứng: Giả định các đường không đồng quy và dẫn dắt đến mâu thuẫn.

Ví Dụ Thực Tế Về Đồng Quy

Để hiểu rõ hơn, hãy xét một vài bài toán thực tế:

Ví Dụ 1: Tìm Các Đường Đồng Quy

Trong bức hình dưới đây, xác định các đường thẳng đồng quy và điểm đồng quy tương ứng.

Các đường p, q, m đồng quy tại điểm A.
Các đường i, p, n đồng quy tại điểm B.

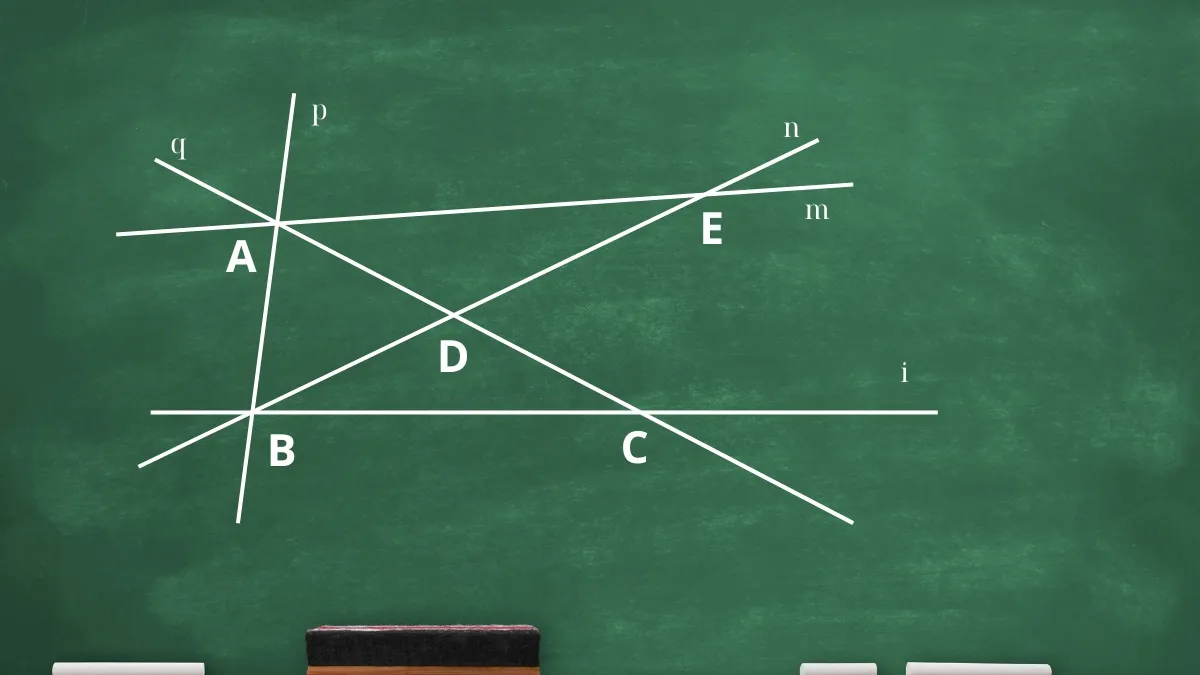Bài tập ví dụ về dạng toán tìm các đường đồng quy

Ví Dụ 2: Chứng Minh Đồng Quy Theo Định Thức

Cho ba phương trình đường thẳng, cần chứng minh chúng đồng quy:

p: 3x – 4y – 13 = 0
q: 8x – 11y – 33 = 0
m: 2x – 3y – 7 = 0

Giải định thức và chứng minh rằng tổng các hệ số bằng không, điều này dẫn đến đồng quy.

Ứng Dụng Của Đồng Quy Trong Thực Tế

Đồng quy không chỉ là lý thuyết mà còn có vai trò quan trọng trong nhiều lĩnh vực:

Kiến Trúc & Xây Dựng: Được sử dụng để thiết kế các cấu trúc chịu lực tốt.
Cơ Học: Áp dụng trong thiết kế máy móc và cơ cấu chuyển động.
Quang Học: Hữu ích trong thiết kế ống kính và máy ảnh.

Ứng dụng của đồng quy trong thực tế

Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về khái niệm 3 đường thẳng đồng quy. Nếu bạn còn câu hỏi nào khác về hình học, đừng ngần ngại tìm kiếm thông tin thêm để làm giàu kiến thức của mình. Đọc thêm về những ứng dụng thực dụng khác tại quặng dolomit là gì để khám phá thêm nhiều điều thú vị.