Thể Tích Hình Trụ – Khám Phá Công Thức và Ứng Dụng Trong Cuộc Sống

Thể tích hình trụ là một trong những khái niệm quan trọng trong toán học, đặc biệt trong chương trình học lớp 12. Hiểu rõ về thể tích hình trụ không chỉ giúp học sinh có thể giải quyết tốt các bài tập toán mà còn ứng dụng vào nhiều lĩnh vực thực tiễn. Bài viết này Chuyenyenbai.edu.vn sẽ cung cấp cho bạn cái nhìn sâu sắc hơn về thể tích hình trụ, từ định nghĩa đến công thức tính toán và ứng dụng của nó.

Thể Tích Hình Trụ: Công Thức và Ứng Dụng

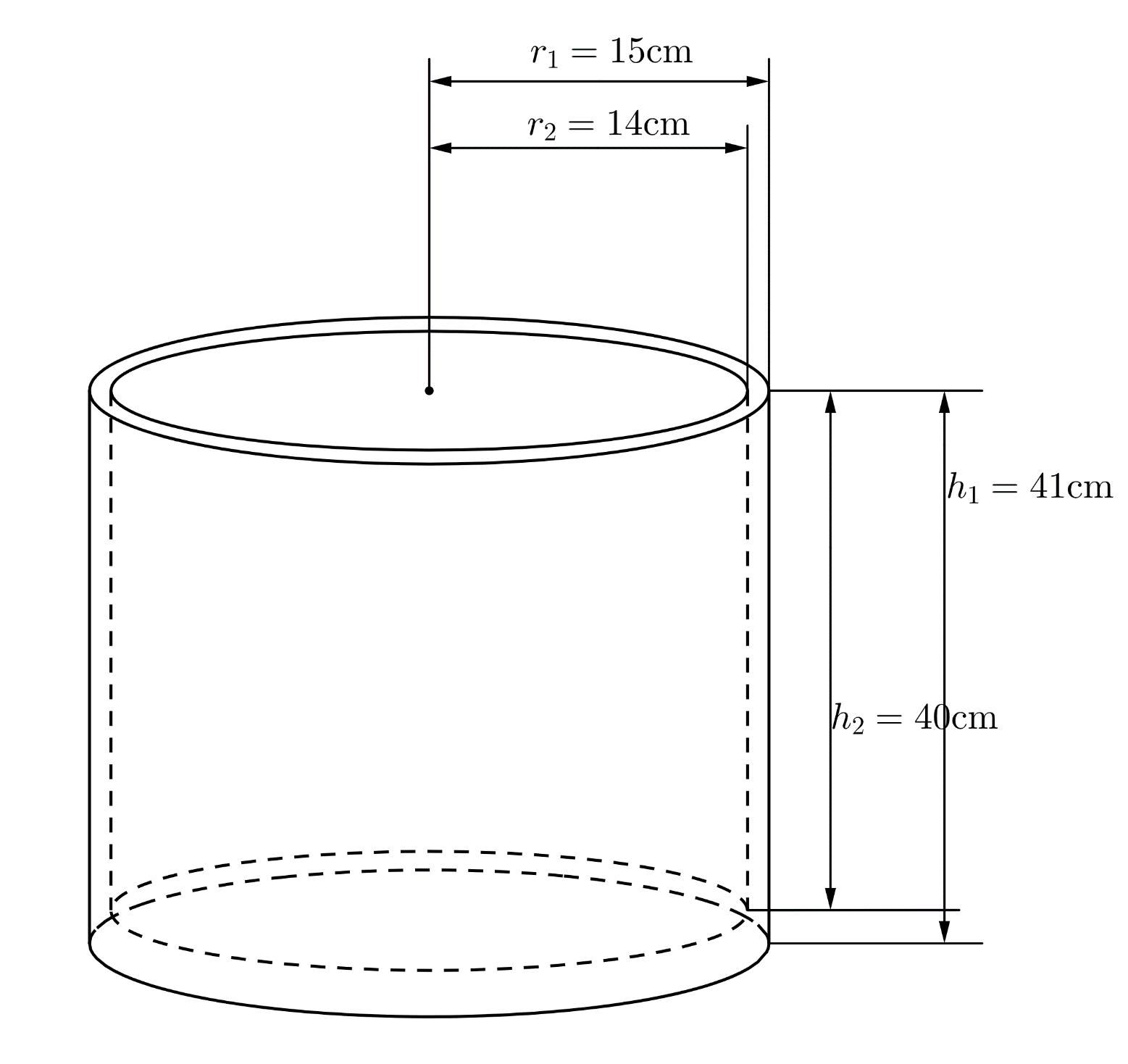
Khi nhắc đến thể tích hình trụ, điều đầu tiên chúng ta nghĩ đến chính là khái niệm cơ bản về hình trụ trong toán học. Hình trụ là một khối hình học được tạo thành từ hai mặt đáy hình tròn song song và một bề mặt bao quanh. Việc tính toán thể tích của hình trụ không chỉ đơn thuần là xác định diện tích đáy và chiều cao mà còn liên quan đến nhiều khía cạnh khác nhau trong thực tế.

Định Nghĩa về Thể Tích Hình Trụ

Để hiểu rõ hơn về thể tích hình trụ, trước tiên chúng ta cần nắm bắt những khái niệm cơ bản liên quan đến nó. Thể tích của khối trụ tròn xoay được định nghĩa là giới hạn của thể tích của khối lăng trụ đều nội tiếp khi số cạnh ở đáy tăng lên vô hạn. Điều này có nghĩa là hình dạng của khối trụ sẽ được làm phẳng khi số lượng mặt đáy càng tăng, và việc tính toán trở nên dễ dàng hơn.

Hình trụ có thể được mô tả bằng nhiều thông số khác nhau như bán kính đáy, chiều cao, diện tích đáy, và thể tích. Những yếu tố này không chỉ giúp chúng ta hình dung về hình dáng hình trụ mà còn hỗ trợ trong việc tính toán cụ thể.

Cách Xác Định Hình Dáng và Kích Thước của Hình Trụ

Hình trụ có thể được hiểu qua các yếu tố cấu thành như bán kính, chiều cao, và diện tích xung quanh. Việc xác định được những yếu tố này rất quan trọng trong quá trình tính toán thể tích.

Chúng ta thường sử dụng công thức V = πr²h để xác định thể tích của hình trụ, trong đó r là bán kính đáy và h là chiều cao. Công thức này giúp người học dễ dàng nhớ và áp dụng vào các bài tập khác nhau.

Ý Nghĩa của Thể Tích trong Thực Tiễn

Thể tích hình trụ không chỉ đơn thuần là một khái niệm lý thuyết mà còn có ý nghĩa rất lớn trong cuộc sống hàng ngày. Chẳng hạn, khi thiết kế một bể chứa nước, việc tính toán thể tích sẽ giúp biết được lượng nước mà bể chứa có thể chứa được. Hay trong ngành xây dựng, thể tích cũng được tính toán để xác định lượng vật liệu cần thiết cho một công trình nào đó.

Công Thức Tính Thể Tích Hình Trụ

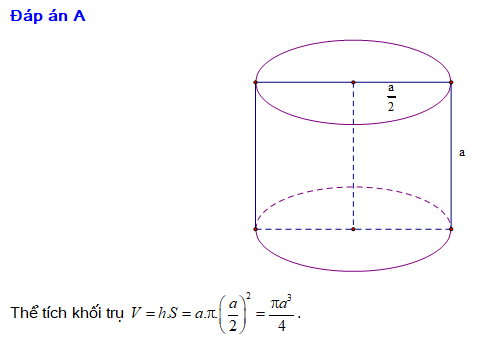
Công thức tính thể tích hình trụ là kiến thức cốt lõi mà mỗi học sinh cần nắm vững để giải quyết các bài tập khó trong đề thi. Trong phần này, chúng ta sẽ đi sâu vào công thức tổng quát cùng với các yếu tố cấu thành nó.

Công Thức Tổng Quát

Như đã đề cập, công thức tính thể tích hình trụ được biểu thị bằng công thức:

[ V = πr²h ]

Trong đó:

• V là thể tích
• r là bán kính đáy của hình trụ
• h là chiều cao của hình trụ

Công thức này cho phép người học dễ dàng tính toán thể tích của bất kỳ hình trụ nào miễn là bạn biết được bán kính đáy và chiều cao.

Giải Thích Các Yếu Tố Trong Công Thức

Mỗi yếu tố trong công thức đều có vai trò riêng của nó. Bán kính đáy (r) phản ánh kích thước của đáy hình trụ, trong khi chiều cao (h) quyết định độ dài của hình trụ. Khi cả hai yếu tố này thay đổi, thể tích cũng sẽ thay đổi theo. Điều này thể hiện rằng kích thước của hình trụ có ảnh hưởng trực tiếp đến thể tích của nó.

Việc hiểu rõ các yếu tố này không chỉ giúp bạn trong việc áp dụng công thức mà còn nâng cao khả năng phân tích và đánh giá tình huống.

Đơn Vị Đo Thể Tích

Đơn vị đo thể tích thường được sử dụng là mét khối (m³), nhưng trong một số trường hợp, thể tích cũng có thể được đo bằng lít (L) hoặc centimét khối (cm³). Việc chuyển đổi giữa các đơn vị này rất quan trọng, đặc biệt là khi bạn làm việc trong các lĩnh vực khoa học hoặc kỹ thuật.

Ví Dụ Minh Họa

Nhằm giúp bạn hiểu rõ hơn về cách áp dụng công thức tính thể tích hình trụ, dưới đây là một số ví dụ minh họa chi tiết.

Ví Dụ 1: Tính Thể Tích Hình Trụ Tròn Xoay

Giả sử bạn có một hình trụ có bán kính đáy là 3 cm và chiều cao là 4 cm.

Thể tích được tính bằng công thức:

[ V = πr²h = π times 3² times 4 ]

Sau khi tính toán, ta nhận được kết quả là:

[ V = 36π text³ ]

Ví Dụ 3: Hình Trụ Nội Tiếp Hai Hình Vuông

Một bài toán thú vị khác liên quan đến hình trụ nội tiếp hai hình vuông. Nếu bạn có hai hình vuông ABCD và A’B’C’D’, cạnh a, và muốn tính diện tích xung quanh và thể tích của hình trụ có hai đáy là hai hình tròn ngoại tiếp hai hình vuông này, bạn cần xác định bán kính đáy của hình trụ.

Bán kính đáy sẽ bằng khoảng cách từ trung điểm đến đỉnh của hình vuông. Sau khi xác định được bán kính và chiều cao, bạn có thể tính toán diện tích xung quanh và thể tích một cách dễ dàng.

Ứng Dụng Thực Tế của Thể Tích Hình Trụ

Thể tích hình trụ không chỉ hữu ích trong các bài toán lý thuyết mà còn có nhiều ứng dụng thực tiễn trong cuộc sống. Bài viết này sẽ tập trung vào ba lĩnh vực chính mà thể tích hình trụ thường được ứng dụng.

Ứng Dụng Trong Ngành Xây Dựng

Trong ngành xây dựng, việc tính toán thể tích là một công việc thiết yếu. Những kiến trúc sư và kỹ sư xây dựng thường xuyên phải xác định thể tích của các khối bê tông, ống dẫn nước, và nhiều cấu trúc khác. Việc xác định đúng thể tích giúp họ có thể ước tính được lượng vật liệu cần thiết cho một dự án, từ đó tiết kiệm thời gian và chi phí.

Ứng Dụng Trong Thiết Kế Sản Phẩm

Trong lĩnh vực thiết kế sản phẩm, kiến thức về thể tích hình trụ cũng rất quan trọng. Ví dụ, khi thiết kế một chai nước hoặc một bình chứa chất lỏng, các nhà thiết kế cần phải tính toán thể tích sao cho phù hợp với nhu cầu sử dụng. Họ cũng phải đảm bảo rằng sản phẩm có thể chứa đủ lượng chất lỏng mong muốn mà không bị tràn ra ngoài.

Ứng Dụng Trong Nghiên Cứu Khoa Học

Trong nghiên cứu khoa học, thể tích hình trụ thường được sử dụng để đánh giá các mẫu vật liệu hoặc các mẫu thử nghiệm. Các nhà khoa học cần xác định chính xác thể tích của các mẫu để tính toán mật độ, hàm lượng hoặc các thông số khác. Kiến thức này không chỉ hỗ trợ trong nghiên cứu mà còn góp phần phát triển các sản phẩm mới trong công nghệ.

Một Số Bài Tập Rèn Luyện Kỹ Năng

Để củng cố kiến thức về thể tích hình trụ, việc thực hành qua các bài tập là rất quan trọng. Dưới đây là một số bài tập từ cơ bản đến nâng cao mà bạn có thể tham khảo.

Bài Tập Cơ Bản

Bài tập đầu tiên có thể là tính thể tích của một hình trụ có bán kính đáy là 5 cm và chiều cao là 10 cm. Đây là một bài tập dễ dàng giúp người học làm quen với công thức.

Bài Tập Nâng Cao

Bài tập nâng cao hơn có thể là tính thể tích của một hình trụ có thiết diện qua trục là hình chữ nhật. Bạn cần xác định chiều cao và bán kính rồi áp dụng công thức để tính toán.

Hướng Dẫn Giải và Phân Tích Bài Tập

Đối với mỗi bài tập, việc hướng dẫn giải và phân tích là rất quan trọng. Bạn có thể viết ra từng bước giải quyết, từ việc xác định các thông số cho đến việc áp dụng công thức và cuối cùng là đưa ra kết quả.

Kết Luận

Thể tích hình trụ không chỉ là một công thức toán học đơn thuần mà còn có nhiều ứng dụng thực tiễn quan trọng trong đời sống hàng ngày cũng như trong các lĩnh vực chuyên môn khác nhau. Việc nắm vững kiến thức này sẽ hỗ trợ người học trong việc giải quyết bài tập toán học và áp dụng vào thực tế hiệu quả hơn. Thông qua bài viết này, hy vọng bạn đã có thêm nhiều thông tin bổ ích về thể tích hình trụ và nguồn cảm hứng để khám phá sâu hơn về môn học này.