Phương pháp nội suy là gì? Tổng quan và ứng dụng chi tiết

Phương pháp nội suy là một công cụ toán học hữu ích trong việc xử lý dữ liệu và dự đoán. Nếu bạn đang tìm hiểu về khái niệm, cách thức hoạt động và ứng dụng của nội suy, bài viết này sẽ giúp bạn có cái nhìn rõ nét và toàn diện.

Phương pháp nội suy là gì?

Khái niệm

Nội suy là một phương pháp toán học nhằm ước lượng giá trị của một hàm số tại các điểm nằm giữa hai hoặc nhiều điểm dữ liệu đã biết. Nó được sử dụng khi bạn muốn dự đoán giá trị nhưng không có số liệu trực tiếp tại những điểm cần tìm. Nội suy rất hữu ích để tối ưu hóa và phân tích dữ liệu rời rạc.

Ví dụ, thay vì thực hiện một thí nghiệm đắt đỏ hoặc đo đạc phức tạp, những công thức nội suy sẽ giúp bạn tính toán và dự đoán giá trị một cách nhanh chóng và chính xác.

Hình minh họa về phương pháp nội suy

Đặc điểm và ứng dụng thực tiễn

Phương pháp nội suy được ứng dụng rộng rãi trong các lĩnh vực như khoa học, kỹ thuật, tài chính, xây dựng và xã hội học. Công cụ này giúp ước lượng giá trị của các điểm dữ liệu chưa được biết dựa trên các thông tin hiện có. Mức độ chính xác của nó sẽ phụ thuộc vào các yếu tố, chẳng hạn như số lượng dữ liệu nguồn, tính liên tục của dữ liệu và loại phương pháp nội suy được sử dụng.

Ứng dụng cụ thể của phương pháp nội suy:

Trắc địa: Lập bản đồ sử dụng dữ liệu vệ tinh, mô phỏng địa hình và xác định các điểm địa lý.
Kỹ thuật: Tiên đoán các tính chất vật liệu tại các điều kiện môi trường khác nhau.
Thống kê: Phân tích dữ liệu rời rạc, xây dựng các mô hình dự báo và bổ sung dữ liệu còn thiếu.
Tài chính: Dự đoán biến động giá, xu hướng thị trường tài chính hoặc phân tích dữ liệu kinh tế.

Các phương pháp nội suy phổ biến hiện nay

Nội suy tuyến tính

Nội suy tuyến tính là cách tiếp cận đơn giản và phổ biến nhất. Phương pháp này dựa trên giả định rằng mối quan hệ giữa hai điểm dữ liệu là tuyến tính.

Công thức nội suy tuyến tính giữa hai điểm dữ liệu ( (x_0, y_0) ) và ( (x_1, y_1) ):

[
y = y_0 + (x – x_0) cdot frac{(y_1 – y_0)}{(x_1 – x_0)}
]

Ứng dụng: Được dùng trong các bài toán đơn giản, ví dụ như dự đoán xu hướng tiêu thụ, phân bổ tài nguyên hoặc đo lường vật lý.

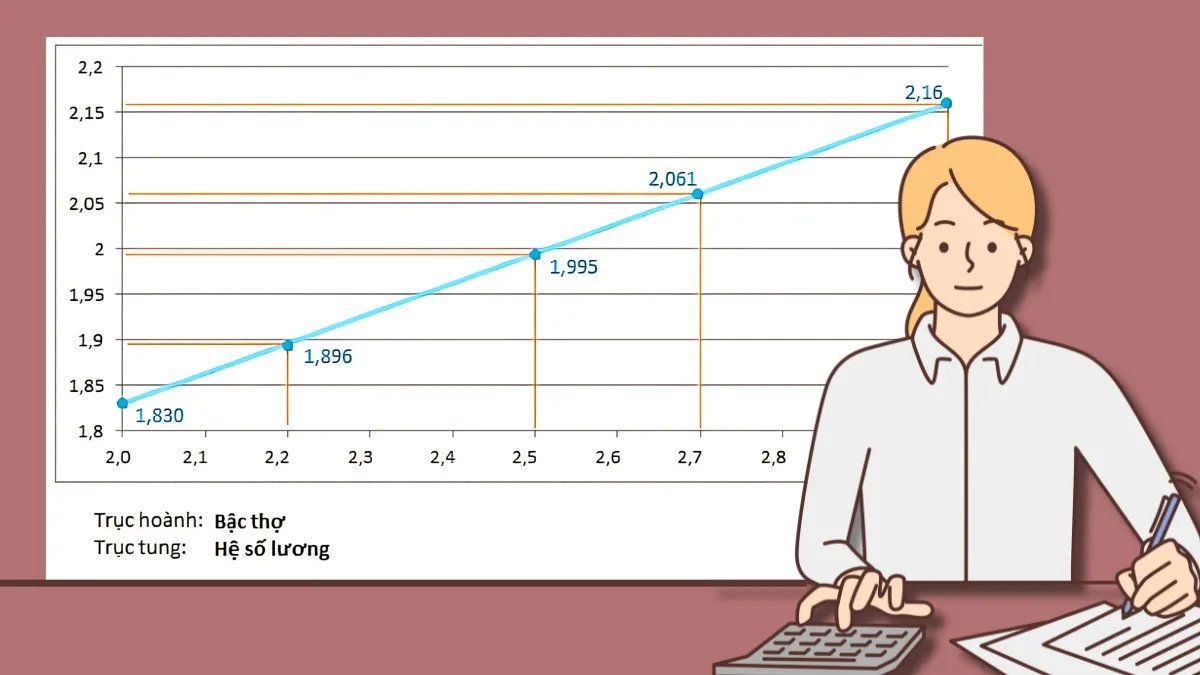Hình minh họa về nội suy tuyến tính

Nội suy Lagrange

Phương pháp nội suy Lagrange giúp tính giá trị tại một điểm bất kỳ dựa trên đa thức đi qua các điểm đã biết. Đây là cách nội suy phù hợp khi bạn làm việc với dữ liệu đa cấp để tăng độ chính xác.

Công thức nội suy Lagrange đối với ( n+1 ) điểm được biểu diễn như sau:

[
P(x) = sum_{i=0}^{n} y_i cdot L_i(x)
]

Trong đó, ( L_i(x) ) là đa thức cơ bản Lagrange.

Ưu điểm: Tăng mức độ chính xác khi xử lý dữ liệu phức tạp như trong kinh tế, khoa học kỹ thuật.

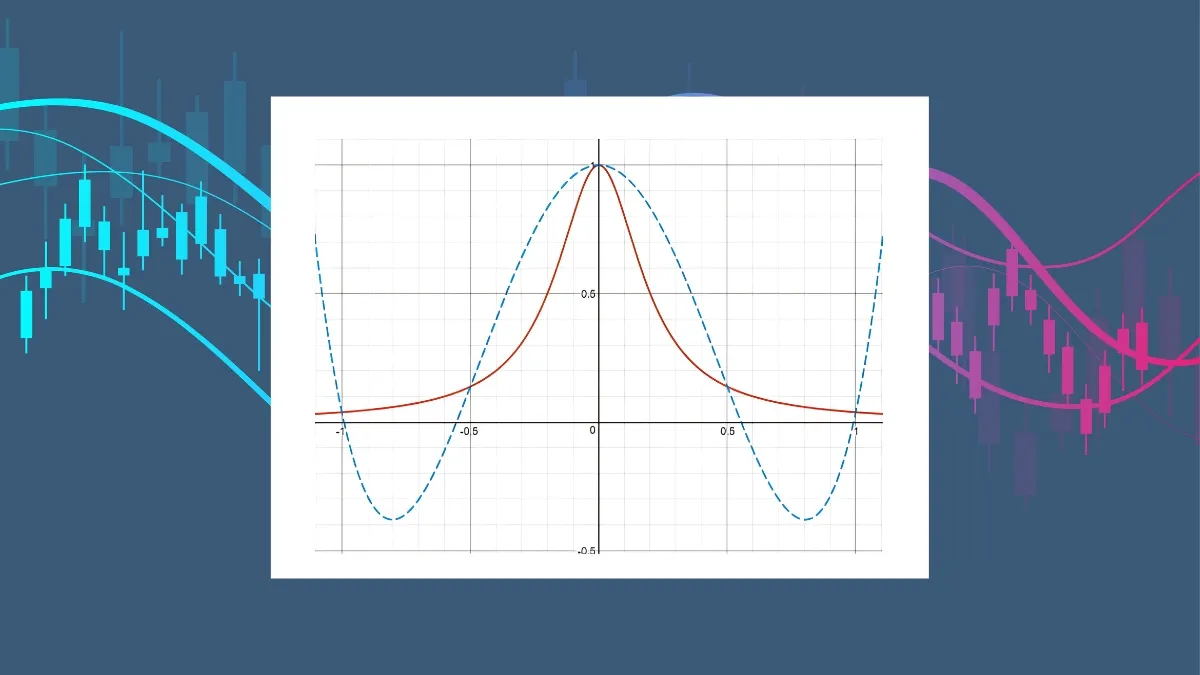Hình minh họa về nội suy Lagrange

Nội suy Newton

Nội suy Newton sử dụng nguyên lý sai phân để tính toán. Nó là một lựa chọn mạnh mẽ để giải quyết các bài toán nội suy phức tạp và có hiệu quả cao khi áp dụng trong các trường hợp dữ liệu phân bố đều.

Một dạng công thức nội suy Newton:

[
P(x) = f[x_0] + (x – x_0)f[x_0, x_1] + ldots + (x – x_0)(x – x1)…(x – x{n-1})f[x_0, x_1, ldots, x_n] ]

Ứng dụng: Thích hợp cho các bài toán kỹ thuật như dự đoán lỗi vật liệu hoặc xây dựng các mô hình toán học chính xác.

Nội suy Spline

Spline là phương pháp dùng các đoạn đường cong hoặc đường thẳng liên tục để kết nối các điểm dữ liệu. Phương pháp này được áp dụng phổ biến trong đồ họa máy tính, thiết kế sản phẩm hoặc các ngành kỹ thuật yêu cầu độ mượt mà và chính xác.

Ưu điểm: Giảm thiểu lỗi đo lường và cải thiện độ mượt mà trong mô hình dữ liệu.

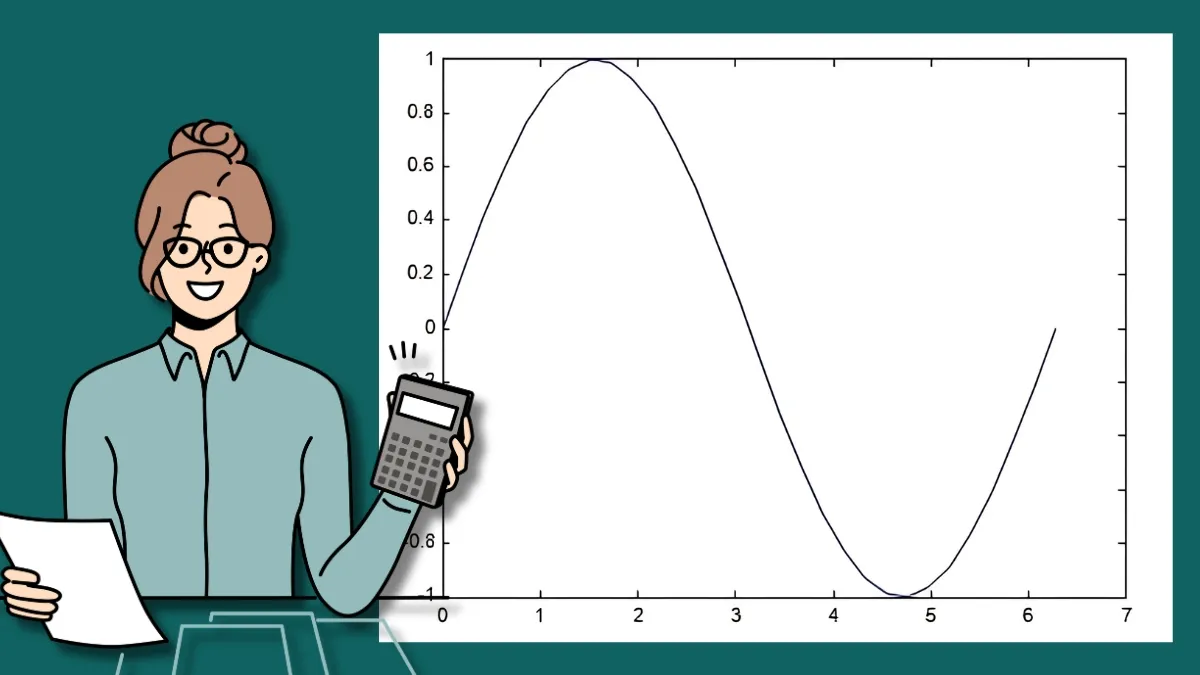Hình minh họa về nội suy Spline

Vai trò của nội suy trong lĩnh vực xây dựng

Trong ngành xây dựng, độ chính xác là yếu tố cốt lõi để đảm bảo chất lượng công trình. Do đó, kỹ sư thường sử dụng các phương pháp nội suy để hỗ trợ tính toán các vấn đề liên quan đến vật liệu, tải trọng và thiết kế.

Ứng dụng cụ thể:

Phân tích độ bền vật liệu: Ước tính các thông số như độ lún, độ co giãn trong điều kiện khác nhau.
Tối ưu chi phí: Hỗ trợ lập kế hoạch xây dựng khi dữ liệu bị thiếu hoặc không đầy đủ.

Hướng dẫn cách áp dụng nội suy tuyến tính trong xây dựng

Dưới đây là các bước cụ thể để áp dụng nội suy tuyến tính:

Chọn các điểm dữ liệu từ tập dữ liệu có sẵn.
Sắp xếp các giá trị theo thứ tự tăng dần.
Tính khoảng cách giữa các điểm liên tục để xác định khu vực nội suy.
Áp dụng công thức nội suy để tính giá trị tại điểm cần tìm.
Kiểm tra kết quả nội suy và so sánh với thông tin thực tế.

Ví dụ: Giả sử bạn muốn ước tính độ dày của lớp vữa tại vị trí 12m, khi các dữ liệu đã có:

Ở vị trí 10m: độ dày vữa là 5mm,
Ở vị trí 15m: độ dày là 7mm.

Áp dụng công thức:

[
y = y_1 + frac{(y_2 – y_1)}{(x_2 – x_1)} cdot (x – x_1)
]

Thay giá trị vào, ta được:

[
y = 5 + frac{(7 – 5)}{(15 – 10)} cdot (12 – 10) = 5,8mm
]

Vậy, độ dày vữa tại vị trí 12m là xấp xỉ 5,8mm.

Những lưu ý cần biết khi sử dụng nội suy

Để đảm bảo kết quả nội suy chính xác, bạn cần tuân thủ các nguyên tắc sau:

Kiểm tra tính đồng nhất của dữ liệu: Loại bỏ giá trị nhiễu để cải thiện kết quả.
Chọn phương pháp phù hợp: Nội suy tuyến tính cho trường hợp đơn giản, nội suy Spline hoặc Lagrange cho dữ liệu phức tạp.
Hạn chế nội suy ngoài phạm vi dữ liệu: Điều này giúp giảm sai số đáng kể.
Dữ liệu đủ lớn: Số lượng điểm dữ liệu càng nhiều, độ chính xác càng cao.

Tài liệu tham khảo:

CellphoneS: biện pháp phi quân sự là gì, biện pháp nghệ thuật là gì

Phương pháp nội suy là gì? Tổng quan và ứng dụng chi tiết