Mod là gì trong toán học? Khái niệm, tính chất và ứng dụng

Mod là một thuật ngữ phổ biến trong toán học, viết tắt của “modulo”. Đây là một phép toán giúp xác định phần dư khi chia một số nguyên cho một số nguyên khác. Hãy cùng tìm hiểu chi tiết hơn về khái niệm, tính chất và cách áp dụng phép toán này trong bài viết sau.

---

Mod là gì trong toán học?

Phép toán modulo, thường được viết ngắn gọn là “mod”, được sử dụng để tìm phần dư của phép chia. Khi chia số nguyên ( a ) cho số nguyên ( b ), phần dư được biểu thị là ( a mod b ). Phép toán này được thực hiện bằng công thức:

[
a mod b = a – (b cdot q)
]

Trong đó ( q ) là phần nguyên của phép chia ( a ) cho ( b ). Ví dụ:

• Nếu chia ( 7 ) cho ( 3 ), ta có kết quả là ( 2 ) (phần nguyên của phép chia). Phần dư sẽ là ( 7 – (3 cdot 2) = 1 ). Do đó: 7 mod 3 = 1.

Vai trò và ứng dụng của modulo

Phép toán modulo được ứng dụng rộng rãi trong nhiều lĩnh vực:

1. Toán học thuần túy:

   • Dùng để nghiên cứu các tính chất chia hết trong lý thuyết số.
   • Giải các bài toán liên quan đến số học modular.

2. Lập trình máy tính:

   • Xác định vị trí của phần tử trong mảng.
   • Thực hiện các thuật toán tính toán dựa trên chu kỳ, như ngày tháng hoặc vòng lặp.

3. Mật mã học:

   • Áp dụng vào các thuật toán mã hóa và giải mã thông tin.

4. Blockchain và hợp đồng thông minh:

   • Sử dụng để tính thời gian hoặc tối ưu hóa giao dịch.

5. Khoa học máy tính:

   • Tính toán trong hashing (băm dữ liệu).
   • Phân tích bảo mật và dữ liệu thông tin.

Nhìn chung, modulo là một công cụ đa năng, vừa hỗ trợ các lĩnh vực học thuật, vừa đóng vai trò quan trọng trong công nghệ hiện đại.

Phép toán modulo

---

Các tính chất quan trọng của mod trong toán học

Các tính chất của phép toán modulo giúp chúng ta thuận tiện hơn khi xử lý bài toán. Dưới đây là một số tính chất tiêu biểu:

1. Tính kết hợp

Cho ba số nguyên bất kỳ ( a, b, c ), ta có:
[
(a mod b) mod c = a mod (b cdot c)
]

2. Tính chia nhỏ

Nếu ( a equiv b mod m ) và ( x equiv y mod m ), thì:

• ((a + x) equiv (b + y) mod m)
• ((a cdot x) equiv (b cdot y) mod m)

3. Tính đối xứng

Hai số nguyên ( a ) và ( b ) thỏa mãn:
[
a equiv b mod m Leftrightarrow b equiv a mod m
]

4. Tính phân phối

Cho ba số nguyên ( a, b, c ), áp dụng phân phối cho phép cộng và nhân:
[
(a + b) mod c = [(a mod c) + (b mod c)] mod c
] [
(a cdot b) mod c = [(a mod c) cdot (b mod c)] mod c
]

5. Phép mũ và modulo

Đối với phép mũ, ta có:
[
a^x mod m = (a mod m)^x mod m
]

6. Tính chia hết

Một số chia hết cho ( m ) khi và chỉ khi:
[
a equiv 0 mod m
]

Các tính chất trên được sử dụng rộng rãi khi giải bài toán liên quan đến modulo, từ lý thuyết số đến ứng dụng thực tiễn.

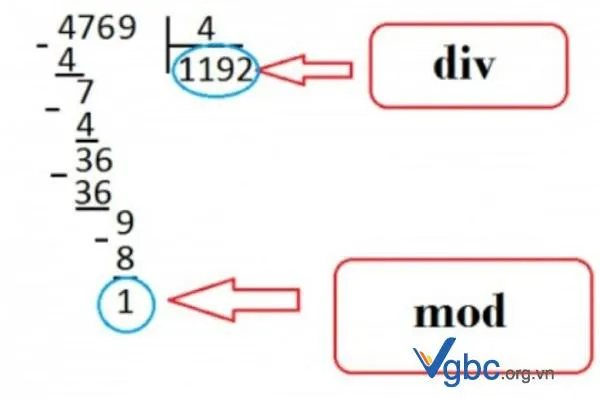Phân tích các bài toán về modulo

---

Các dạng bài tập thường gặp về mod trong toán học

1. Tính phần dư

Đây là dạng bài tập tiêu biểu khi tìm ( a mod b ). Ví dụ:

• Tính ( 123456789 mod 10 ). Ta lấy phần dư của phép chia, kết quả là ( 9 ).

2. Kiểm tra tính chia hết

Sử dụng phép toán modulo để kiểm tra:

• Một số chia hết cho ( 2 ) khi ( a mod 2 = 0 ).

3. Tìm chu kỳ của một dãy số

Dạng bài này tìm chu kỳ lặp lại khi áp dụng modulo. Ví dụ:

• Xác định chu kỳ của dãy Fibonacci với ( mod 10 ).

4. Giải mã thông điệp mã hóa

Trong mật mã học, phép toán modulo giúp giải mã các thông điệp bằng khóa đặc biệt.

5. Xác định ngày trong tuần

Bạn có thể áp dụng phép toán modulo để xác định thứ trong tuần dựa trên một ngày nhất định trong năm.

6. Các bài toán trong lập trình và khoa học máy tính

Ví dụ: sử dụng modulo trong hệ thống nhị phân để tối ưu hóa các thuật toán.

Các dạng bài tập trên chỉ là vài ví dụ đơn giản. Tùy thuộc vào hoàn cảnh, bài toán có thể đòi hỏi những cách tiếp cận khác nhau.

---

Kết luận

Phép toán modulo (mod) không chỉ là một công cụ trong toán học mà còn là nền tảng nhiều lĩnh vực công nghệ như lập trình, mật mã học và blockchain. Việc nắm vững khái niệm và ứng dụng của phép toán này sẽ giúp bạn giải quyết hiệu quả các bài toán học thuật và thực tế.

Bạn có thể tìm hiểu thêm về các thuật ngữ toán học khác như lg là gì trong toán học hoặc khám phá thông tin mới tại chuyên mục giáo dục của chúng tôi.

Hãy đặt câu hỏi hoặc khám phá thêm về kiến thức của toán học để nâng cao hiểu biết!

Xem thêm: Ctrl + Shift + N là gì.