Tứ giác là gì? Khám phá định nghĩa, phân loại và bí quyết học toán hiệu quả

Tứ Giác Là Gì? Đây là câu hỏi mà nhiều học sinh đặt ra khi bắt đầu tìm hiểu về hình học trong chương trình toán học. Tứ giác là một trong những hình học cơ bản và được áp dụng phổ biến trong các bài học và bài thi. Trong bài viết này, hãy cùng khám phá khái niệm tứ giác, phân loại, tính chất, công thức và cách học hiệu quả liên quan đến hình tứ giác.

Tứ giác là gì?

Tứ giác, hay hình tứ giác, là một đa giác có 4 đỉnh và 4 cạnh. Mỗi cạnh của tứ giác là một đoạn thẳng kết nối giữa hai đỉnh kề nhau, và không có bất kỳ cặp đoạn thẳng nào nằm trên cùng một đường thẳng. Điều này tạo nên hình dáng đặc biệt của tứ giác trong hình học.

Hình minh họa tứ giác cơ bản
Hình minh họa tứ giác cơ bản: Một đa giác với 4 đỉnh và 4 cạnh

Tính chất cơ bản của tứ giác

Để hiểu rõ hơn về hình tứ giác, cần nắm vững một số tính chất cơ bản như sau:

Tổng các góc trong tứ giác:
Tổng các góc trong của một hình tứ giác luôn bằng 360°, bất kể là tứ giác lồi hay tứ giác lõm. Công thức:
- ∠A + ∠B + ∠C + ∠D = 360°.
Tính chất của đường chéo:
- Đối với tứ giác lồi, hai đường chéo sẽ giao nhau tại một điểm nằm bên trong tứ giác.
- Nếu hai đường chéo của tứ giác giao nhau tại một điểm bên trong tứ giác, hình đó là tứ giác lồi.

Phân loại tứ giác và cách nhận biết

Tứ giác được phân thành nhiều loại khác nhau, với mỗi loại đều có những đặc điểm riêng biệt. Dưới đây là cách phân loại phổ biến cùng phương pháp nhận biết.

1. Tứ giác đơn

Đặc điểm: Là hình học cơ bản trong tứ giác, không có cạnh nào cắt nhau.
Nhận biết: Các cạnh chỉ giao nhau tại các đỉnh và không chồng chéo lên nhau.

2. Tứ giác lồi

Đặc điểm: Cả 4 góc đều nhỏ hơn 180° và hai đường chéo đều nằm trọn trong hình.
Nhận biết: Khi kéo dài các cạnh, tứ giác lồi sẽ hoàn toàn nằm trong vùng bao quanh bởi các cạnh này.

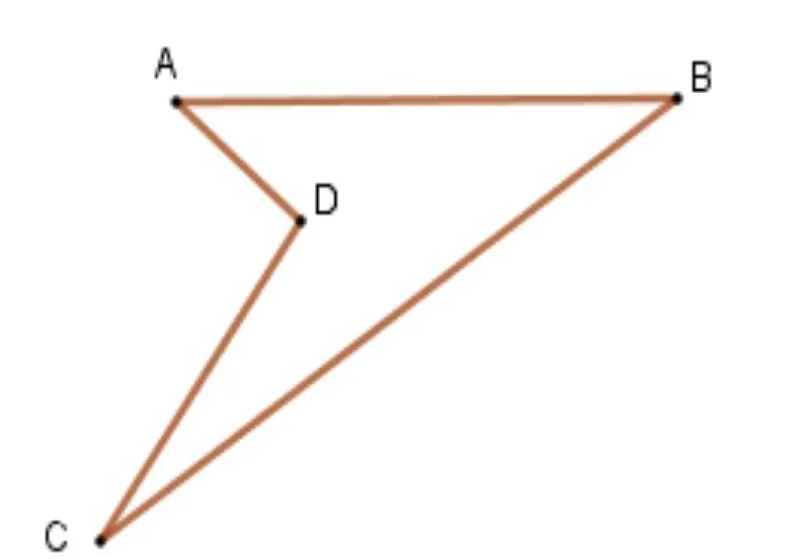
3. Tứ giác lõm

Đặc điểm: Có ít nhất một góc lớn hơn 180°, và một trong các đường chéo sẽ nằm bên ngoài hình.
Nhận biết: Kéo dài các cạnh, sẽ có phần của tứ giác nằm bên ngoài vùng bao quanh bởi các cạnh.

Hình minh họa tứ giác lồi
Hình minh họa tứ giác lồi: Mọi góc đều nhỏ hơn 180°, các đường chéo nằm hoàn toàn bên trong hình

Các dạng hình tứ giác đặc biệt

Trong toán học, ngoài các dạng tứ giác cơ bản, còn có một số hình tứ giác đặc biệt mà học sinh cần nắm bắt, bao gồm:

1. Hình thang
Hình thang là một loại tứ giác có ít nhất hai cạnh đối song song.

2. Hình thang cân
Hình thang cân là một trường hợp đặc biệt của hình thang. Các tính chất nổi bật:

Hai góc kề nằm trên cùng một cạnh đáy có số đo bằng nhau.
Hai đường chéo của hình thang cân dài bằng nhau.

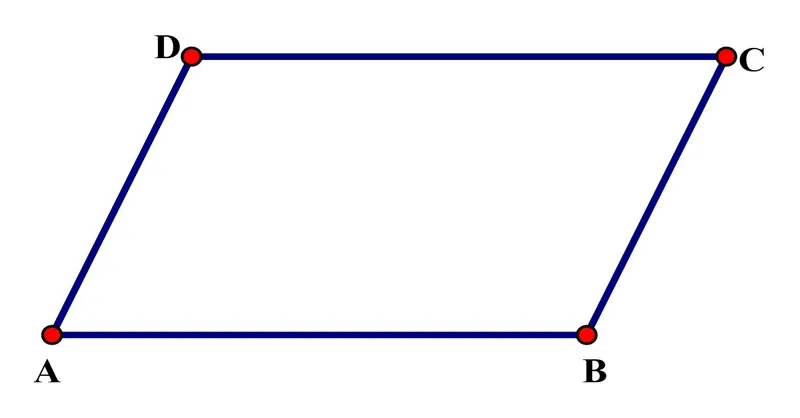
3. Hình bình hành
Hình bình hành là một loại tứ giác với các tính chất:

Hai cặp cạnh đối song song và có độ dài bằng nhau.
Góc đối bằng nhau, và các đường chéo cắt nhau tại trung điểm của mỗi đường.

4. Hình chữ nhật
Hình chữ nhật có đặc điểm:

Bốn góc đều là góc vuông.
Hai cặp cạnh đối song song và dài bằng nhau.
Hai đường chéo cũng bằng nhau và cắt nhau tại trung điểm của cả hai.

Hình vuông và hình chữ nhật
Hình minh họa cho các dạng hình tứ giác đặc biệt như hình vuông, hình chữ nhật

5. Hình vuông
Hình vuông là một dạng kết hợp giữa hình chữ nhật và hình thoi, với các cạnh bằng nhau và tất cả các góc đều vuông.

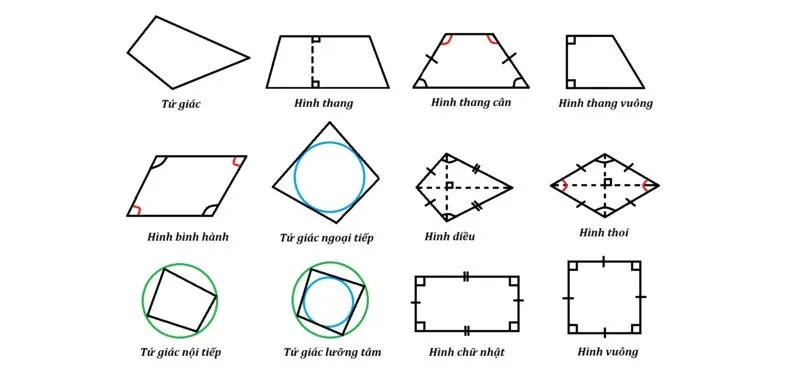
6. Tứ giác nội tiếp
Tứ giác nội tiếp có 4 đỉnh nằm trên cùng một đường tròn. Trong trường hợp này:

Đường tròn bao quanh đi qua tất cả các đỉnh.
Tâm của đường tròn là tâm ngoại tiếp, bán kính gọi là bán kính ngoại tiếp của hình.

Công thức tính toán với hình tứ giác

Hình tứ giác thường được áp dụng trong việc tính chu vi và diện tích. Dưới đây là các công thức cơ bản:

1. Công thức tính chu vi

Chu vi của tứ giác là tổng chiều dài 4 cạnh. Công thức:

P = a + b + c + d, với a, b, c, d lần lượt là độ dài các cạnh.

2. Công thức tính diện tích

Diện tích tứ giác thay đổi tùy theo từng dạng hình:

Hình vuông:
- S = a × a, với a là chiều dài một cạnh.
Hình chữ nhật:
- S = a × b, với a là chiều dài và b là chiều rộng.
Hình bình hành:
- S = a × h, với a là cạnh đáy và h là độ cao.

Bí quyết học hiệu quả kiến thức về tứ giác

1. Nắm chắc kiến thức cơ bản

Học sinh cần tự đặt mục tiêu hiểu rõ định nghĩa, phân loại, tính chất, và công thức tính chu vi, diện tích của mỗi loại tứ giác. Đây chính là nền tảng để giải quyết các bài tập nâng cao.

2. Học thực hành qua bài tập

Áp dụng lý thuyết vào thực tế là cách tốt nhất để ghi nhớ:

Giải bài tập dễ trước: Tạo thói quen làm các bài tập đơn giản về tính chu vi, diện tích trước.
Tiếp cận bài tập nâng cao: Các dạng bài yêu cầu tư duy phức tạp giúp học sinh phát triển khả năng giải toán toàn diện.

Trẻ học toán với hình ảnh sinh động
Ứng dụng học tập giúp trẻ dễ dàng hiểu bài hơn thông qua hình ảnh sinh động

3. Kết hợp công nghệ

Cha mẹ và giáo viên có thể thử các ứng dụng học toán trực tuyến như VioEdu hoặc Monkey Math. Các ứng dụng này mang lại góc nhìn trực quan, từ đó giúp trẻ dễ dàng tiếp thu kiến thức toán học.

Lời kết

Hình tứ giác không chỉ là một khái niệm cơ bản mà còn là yếu tố quan trọng trong việc phát triển các kỹ năng giải toán của học sinh. Hy vọng bài viết đã giúp bạn hiểu rõ “tứ giác là gì”, cùng những kiến thức cần thiết liên quan đến nó. Hãy tiếp tục rèn luyện và khám phá các dạng bài tập khác nhau để áp dụng hiệu quả những gì đã học nhé!

Bên cạnh đó, để hỗ trợ con bạn học tập, có rất nhiều nền tảng casino trực tuyến đáng tin cậy ứng dụng công nghệ số để giúp trẻ nâng cao kỹ năng toán học và tư duy logic. Hãy tham khảo thêm các cách làm bình đắp đá tự chế hay các bài viết bổ ích liên quan nhé!

Tứ giác là gì? Khám phá định nghĩa, phân loại và bí quyết học toán hiệu quả